ಅಭ್ಯಾಸ 2.1
ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳಲ್ಲಿ ಯಾವುದು ಸತ್ಯ ಮತ್ತು ಯಾವುದು ಸುಳ್ಳು? ನಿಮ್ಮ ಉತ್ತರಕ್ಕೆ ಕಾರಣಗಳನ್ನು ಕೊಡಿರಿ.
(i) ಒಂದು ಬಿಂದುವಿನ ಮೂಲಕ ಒಂದೇ ಒಂದು ಸರಳರೇಖೆ ಹಾದು ಹೋಗಬಹುದು.
Ans:-ಸತ್ಯವಲ್ಲ
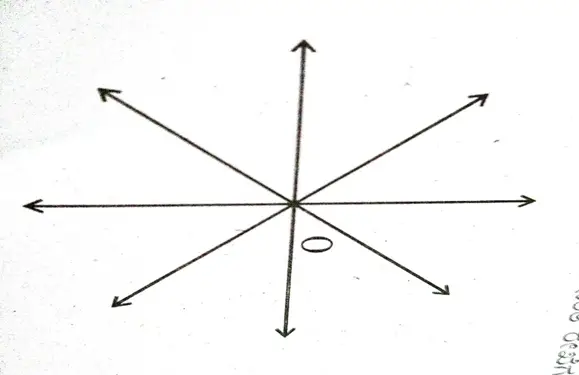
ಏಕೆಂದರೆ ಒಂದು ಬಿಂದುವಿನ ಮೂಲಕ ಅನಂತ ರೇಖೆಗಳು ಹಾದು ಹೋಗಬಹುದು.
(ii) ಎರಡು ಪ್ರತ್ಯೇಕ ಬಿಂದುಗಳ ಮೂಲಕ ಅಪರಿಮಿತ ರೇಖೆಗಳು ಹಾದು ಹೋಗುತ್ತವೆ.
Ans:-ಸತ್ಯವಲ್ಲ
ಏಕೆಂದರೆ ಪ್ರತ್ಯೇಕ ಬಿಂದುಗಳ ಮೂಲಕ ಒಂದೇ ಒಂದು ರೇಖೆಯು ಹಾದು ಹೋಗುತ್ತದೆ.

(iii) ಒಂದು ಅಂತ್ಯಗೊಂಡಿರುವ ರೇಖೆಯನ್ನು ಎರಡೂ ಬದಿಗಳಲ್ಲಿ ಅನಿರ್ದಿಷ್ಟವಾಗಿ ವೃದ್ಧಿಸಬಹುದು.
Ans:-ಸತ್ಯ.
ಏಕೆಂದರೆ ಒಂದು ಅಂತ್ಯಗೊಂಡಿರುವ ರೇಖೆಯನ್ನು ಎರಡೂ ಬದಿಗಳಲ್ಲಿ ಅನಂತವಾಗಿ ವೃದ್ಧಿಸಬಹುದು.

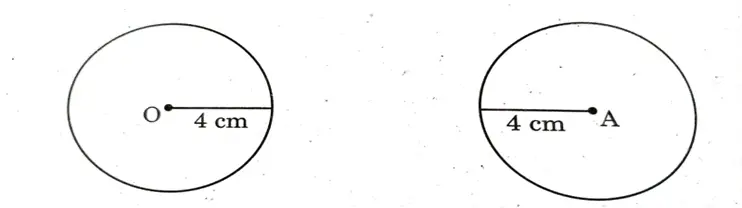
(iv) ಎರಡು ವೃತ್ತಗಳು ಸಮ ಎಂದಾದರೆ, ಅವುಗಳ ತ್ರಿಜ್ಯಗಳೂ ಸಮವಾಗಿರುತ್ತವೆ.
Ans:-ಸತ್ಯ.
ಏಕೆಂದರೆ ಆ ವೃತ್ತಗಳ ಕೇಂದ್ರ, ಪರಿದಿ ಹಾಗೂ ತ್ರಿಜ್ಯಗಳು ಒಂದೇ ಆಗಿರುತ್ತವೆ.
(v) ಚಿತ್ರ 5.9 ರಲ್ಲಿ, AB = PQ ಮತ್ತು PQ = XY, ಎಂದಾದರೆ AB=XY ಆಗಿರುತ್ತದೆ.
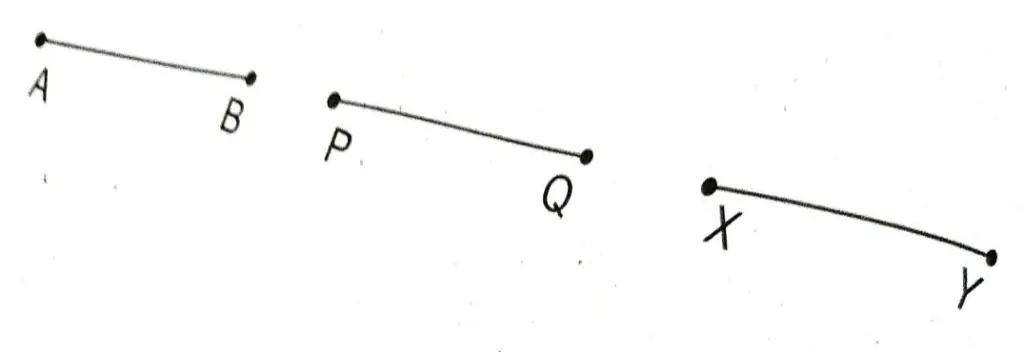
Ans:- ಸತ್ಯ.
AB = PQ
XY = PQ
AB = XY
ಯೂಕ್ಲಿಡ್ನ ಮೊದಲ ಸ್ವಯಂ ಸಿದ್ಧದಂತೆ “ಒಂದೇ ಅಂಶಕ್ಕೆ ಸಮನಾಗಿರುವ ಅಂಶಗಳು ಒಂದಕ್ಕೊಂದು ಸಮ”.
2.ಕೆಳಗಿನ ಪ್ರತಿಯೊಂದು ಪದಕ್ಕೂ ಒಂದೊಂದು ವ್ಯಾಖ್ಯೆಯನ್ನು ನೀಡಿರಿ. ಪ್ರಥಮದಲ್ಲಿ ಬೇರೆ ಯಾವುದಾದರೂ ಪದಗಳನ್ನು ಇದ್ದರೆ ಅವುಗಳು ಯಾವುವು? ನೀವು ಅವುಗಳನ್ನು ಹೇಗೆ ವ್ಯಾಖ್ಯಾನಿಸುವಿರಿ?
(i) ಸಮಾಂತರ ರೇಖೆಗಳು
ಪರಿಹಾರ :
ಒಂದೇ ಸಮತಲದ ಮೇಲೆ ಇರುವ ಎರಡು ಸರಳ ರೇಖೆ ಗಳನ್ನು ಎರಡು ಕಡೆಯು ವೃದ್ಧಿಸಿದಾಗ ಒಂದಕ್ಕೊಂದು ಛೇದಿಸದ ರೇಖೆಗಳಾದರೆ ಅವುಗಳನ್ನು ಸಮಾನಾಂತರ ಸರಳ ರೇಖೆಗಳು ಎನ್ನುವರು.

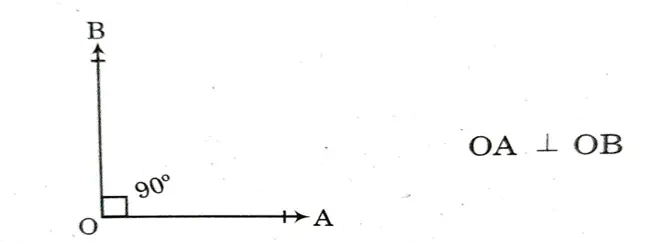
(ii) ಲಂಬರೇಖೆಗಳು
ಉತ್ತರ : ಯಾವ ಎರಡು ರೇಖೆಗಳು ಪರಸ್ಪರ 90° ಯಲ್ಲಿ ಛೇದಿಸುತ್ತವೆಯೋ ಆ ರೇಖೆಗಳನ್ನು ಲಂಬ ಲಂಬರೇಖೆಗಳು ಎನ್ನುವರು.
(iii) ರೇಖಾಖಂಡ
ಉತ್ತರ : ಎರಡು ಬಿಂದುಗಳ ನಡುವೆ ಎಳೆದ ಮತ್ತು ಎರಡು ಕಡೆಯು ವೃದ್ಧಿಸಲಾಗದ ಸರಳ ರೇಖೆಯನ್ನು ರೇಖಾಖಂಡ ಎನ್ನುವರು.

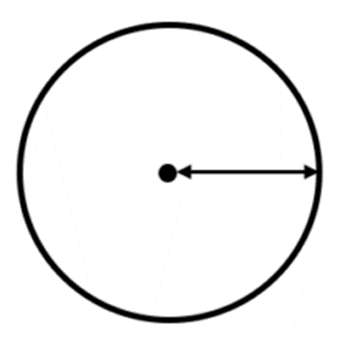
(iv) ಒಂದು ವೃತ್ತದ ತ್ರಿಜ್ಯ
ಉತ್ತರ : ವೃತ್ತ ಕೇಂದ್ರ ಮತ್ತು ಪರಿದಿಯ ಮೇಲಿನ ಯಾವುದಾದರೊಂದು ಬಿಂದುವನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡಕ್ಕೆ ತ್ರಿಜ್ಯ ಎನ್ನುವರು.
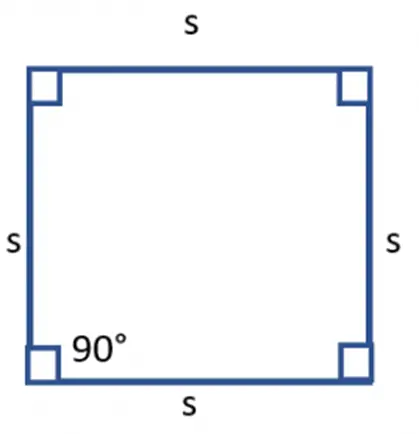
(v)ಚೌಕ
ಉತ್ತರ : ಎಲ್ಲಾ ಬಾಹುಗಳು ಸಮವಾಗಿರುವ ಮತ್ತು ಪ್ರತಿ ಕೋನವು 90° ಇರುವ ಚತುರ್ಭುಜವನ್ನು ಚೌಕ ಮತ್ತು ಅಥವಾ ವರ್ಗ ಎನ್ನುವರು.
3.ಕೆಳಗೆ ನೀಡಿದ ಎರಡು ‘ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳನ್ನು‘ ಗಮನಿಸಿ.
(i) A ಮತ್ತು B ಎಂಬ ಎರಡು ಪ್ರತ್ಯೇಕ ಬಿಂದುಗಳನ್ನು ನೀಡಿದಾಗ, ಅವುಗಳ ನಡುವೆ “ ಎಂಬ 3 ನೇಯ ಬಿಂದು ಇರುತ್ತದೆ.
(ii) ಏಕರೇಖಾಗತವಲ್ಲದಿರುವ ಕನಿಷ್ಠ ಮೂರು ಬಿಂದುಗಳಾದರೂ ಇರುತ್ತವೆ.
ಈ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸದಿರುವ ಯಾವುದಾದರೂ ಪದಗಳಿವೆಯೆ? ಈ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳು ಸುಸಂಗತವೆ? ಅವುಗಳು ಯೂಕ್ಲಿಡನ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳಿಗೆ ಸರಿಹೊಂದುತ್ತವೆಯೇ? ವಿವರಿಸಿ.
ಪರಿಹಾರ :
(i) ದತ್ತ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯಲ್ಲಿ ಬಹಳಷ್ಟು ವ್ಯಾಖ್ಯಾನಿಸಲ್ಲದ ಪದಗಳು.
(ii) ಅವು ಎರಡು ಬೇರೆ ಬೇರೆ ಸನ್ನಿವೇಶಗಳಿಗೆ ಅನ್ವಯಿಸುವುದರಿಂದ, ಈ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳು ಸ್ಥಿರ ಅಥವಾ ಸುಸಂಗತವಾಗಿವೆ.
ಈ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳು ಯೂಕ್ಲಿಡ್ನ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಗಳಂತಿಲ್ಲ. ಆದರೆ ಅವು ಸ್ವಯಂ ಸಿದ್ಧಗಳಿಂದಾಗಿವೆ. “ಎರಡು ದತ್ತ ವಿಭಿನ್ನ ಬಿಂದುಗಳ ಮೂಲಕ ಒಂದೇ ಒಂದು ರೇಖೆಯು ಹಾದು ಹೋಗುತ್ತದೆ“.
4.AC = BC ಆಗುವಂತೆ A ಮತ್ತು B ಬಿಂದುಗಳ ನಡುವೆ C ಎಂಬ ಬಿಂದು ಇರುವುದಾದರೆ, AC = AB/2 ಎಂದು ಸಾಧಿಸಿರಿ. ಚಿತ್ರವನ್ನು ರಚಿಸುವ ಮೂಲಕ ವಿವರಿಸಿ.

(i) AC = BC (ದತ್ತ)
AC ಯನ್ನು ಎರಡು ಕಡೆಯು ಕೂಡಿದಾಗ
AC+AC=BC + AC—————— (1)
ಸಮವಾಗಿರುವ ಅಂಶಗಳಿಗೆ ಸಮವಾಗಿರುವ ಅಂಶಗಳನ್ನು ಕೂಡಿದಾಗ ಮೊತ್ತಗಳು ಸಮವಾಗುತ್ತವೆ.
ಆದರೆ BC + AC = AB
ಆದರೆ,
AC + AC=AB
2 AC = AB .
AC = AB/2
5.4ನೆಯ ಪ್ರಶ್ನೆಯಲ್ಲಿ C ಬಿಂದುವನ್ನು ರೇಖಾಖಂಡ AB ಯ ಮಧ್ಯಬಿಂದು ಎನ್ನುತ್ತೇವೆ. ಪ್ರತಿಯೊಂದು ರೇಖಾಖಂಡಕ್ಕೂ ಒಂದು ಮತ್ತು ಒಂದೇ ಒಂದು ಮಧ್ಯಬಿಂದು ಇರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ :

ಸಾಧನೆ : C ಮತ್ತು D ಎರಡೂ ಬಿಂದುಗಳನ್ನು AB ಯ ಮಧ್ಯಬಿಂದುಗಳೆಂದು ಪರಿಗಣಿಸೋಣ.
Cಯು AB, ಯ ಮಧ್ಯಬಿಂದುವಾದರೆ, AC = CB
ಎರಡು ಕಡೆ AC ಯನ್ನು ಸೇರಿಸಿದಾಗ,
ಸಮವಾಗಿರುವ ಅಂಶಗಳಿಗೆ ಸಮವಾಗಿರುವ ಅಂಶಗಳನ್ನು ಕೂಡಿದಾಗ ಮೊತ್ತಗಳು ಸಮವಾಗುತ್ತವೆ.
AC + AC = BC + AC ,
ಆದರೆ BC + AC = AB
ಈಗ
2AC = AB
2AC =AB
AC=AB/2————————–(1)
AB ಯ ಮಧ್ಯಬಿಂದು D ಆದರೆ, ಆಗ
AD=DB
AD ಯನ್ನು ಎರಡು ಕಡೆಯು ಸೇರಿಸಿದಾಗ,
ಸಮವಾಗಿರುವ ಅಂಶಗಳಿಗೆ ಸಮವಾಗಿರುವ ಅಂಶಗಳನ್ನು ಕೂಡಿದಾಗ ಮೊತ್ತಗಳು ಸಮವಾಗುತ್ತವೆ.
AD + AD = BD + AD
ಆದರೆ,
BD + AD = AB
ಈಗ, 2 AD = AB
AD=AB/2————————(2)
(1)ಮತ್ತು (2) ಸಮೀಕರಣಗಳಿಂದ,
ಸ್ವಯಂಸಿದ್ದ ಒಂದೇ ಅಂಶಕ್ಕೆ ಸಮನಾಗಿರುವ ಅಂಶಗಳು ಒಂದಕ್ಕೊಂದು ಸಮನಾಗಿರುತ್ತವೆ.
AC = AD
ಇದು ‘C’ ಮತ್ತು ‘D’ ಗಳು ಒಂದೇ ಬಿಂದುವಾಗಿದ್ದಾಗ ಮಾತ್ರ ಸಾಧ್ಯ.
ಆದ್ದರಿಂದ ನಮ್ಮ ಪರಿಗಣನೆ ತಪ್ಪು, ದತ್ತ ರೇಖಾಖಂಡಕ್ಕೆ ಒಂದು ಮತ್ತು ಒಂದೇ ಒಂದು ಮಧ್ಯಬಿಂದು ಇರುತ್ತದೆ.
6.ಚಿತ್ರದಲ್ಲಿ, AC = BD ಆದರೆ AB = CD ಎಂದು ಸಾಧಿಸಿ.

ಸಾಧನೆ : ಈ ಮೇಲ್ಕಂಡ ಚಿತ್ರದಂತೆ
AC = AB+BC
BD=CD+BC
ಆದರೆ AC = BD.
“ಸ್ವಯಂ ಸಿದ್ಧ ಒಂದೇ ಅಂಶಕ್ಕೆ ಸಮನಾಗಿರುವ ಅಂಶಗಳು ಒಂದಕ್ಕೊಂದು ಸಮ“
AB+BC=CD+BC
ಸಮಾನ ಅಂಶಗಳಿಂದ, ಸಮಾನ ಅಂಶಗಳನ್ನು ಕಳೆದಾಗ ಉಳಿದ ಭಾಗಗಳು ಸಮವಾಗಿರುತ್ತವೆ.
AB+BC-BC=CD+BC-BC
AB=CD
7.ಯೂಕ್ಲಿಡನ ಸ್ವಯಂಸಿದ್ಧಗಳ ಪಟ್ಟಿಯಲ್ಲಿ, 5ನೇ ಸ್ವಯಂಸಿದ್ದವನ್ನು “ಸಾರ್ವತ್ರಿಕ ಸತ್ಯ” ಎಂದು ಯಾಕೆ ಪರಿಗಣಿಸಲಾಗಿದೆ? (ಪ್ರಶ್ನೆಯು 5ನೇ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯ ಬಗ್ಗೆ ಅಲ್ಲ ಎಂಬುದನ್ನು ಗಮನಿಸಿ)
ಉತ್ತರ :
ಸ್ವಯಂ ಸಿದ್ಧ – 5
ಪೂರ್ಣವು ಭಾಗಕ್ಕಿಂತ ದೊಡ್ಡದು.
ಈ ಸ್ವಯಂ ಸಿದ್ಧವನ್ನು ಸಾರ್ವತ್ರಿಕ ಸತ್ಯ ಎಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ ಏಕೆಂದರೆ ಉಳಿದೆಲ್ಲ ಸ್ವಯಂ
ಸಿದ್ಧಗಳು ಪರೋಕ್ಷವಾಗಿ ಇದರ ಮೇಲೆ ಆಧಾರಿತವಾಗಿದೆ. ಇದು ಎಲ್ಲ ಕ್ಷೇತ್ರಗಳಿಗು ಅನ್ವಯವಾಗುತ್ತದೆ.
ಅಭ್ಯಾಸ 2.2
1.ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಸುಲಭವಾಗುವಂತೆ, ಯೂಕ್ಲಿಡನ 5ನೆಯ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯನ್ನು ನೀವು ಹೇಗೆ ಬದಲಾಯಿಸಿ ಬರೆಯುವಿರಿ?
ಪರಿಹಾರ :
ಆಧಾರ ಪ್ರತಿಜ್ಞೆ– 5
ಎರಡು ಸರಳರೇಖೆಗಳ ಮೇಲೆ ಇನ್ನೊಂದು ಸರಳರೇಖೆ ಬಿದ್ದಾಗ, ಅದರ ಒಂದೇ ಬದಿಯಲ್ಲಿರುವ ಅಂತಃ ಕೋನಗಳನ್ನು ಒಟ್ಟಿಗೆ ತೆಗೆದುಕೊಂಡಾಗ 2 ಲಂಬಕೋನಗಳಿಗಿಂತ ಕಡಿಮೆ ಬಂದರೆ, ಮೊತ್ತವು 2 ಲಂಬಕೋನಗಳಿಗಿಂತ ಕಡಿಮೆ ಬರುವ ದಿಕ್ಕಿನಲ್ಲೇ ಆ ಎರಡು ಸರಳ ರೇಖೆಗಳನ್ನು ಅನಿರ್ದಿಷ್ಟವಾಗಿ ವೃದ್ಧಿಸಿದಾಗ ಅವುಗಳು ಒಂದನ್ನೊಂದು ಸಂಧಿಸುತ್ತವೆ.
ಯೂಕ್ಲಿಡನ 5ನೇ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯ 2 ಸಮಾನ ರೂಪಗಳು.
(i) ಪ್ರತಿಯೊಂದು ರೇಖೆ (l) ಗೆ ಮತ್ತು (l) ನ ಮೇಲಿರುವ ಪ್ರತಿಯೊಂದು ಬಿಂದು (P) ಗೆ, (l)ಗೆ ಸಮಾಂತರವಾಗಿರುವಂತೆ, Pಯ ಮೂಲಕ ಹಾದುಹೋಗುವ ‘m’ ಎಂಬ ಒಂದೇ ಒಂದು ರೇಖೆ ಇರುತ್ತದೆ.
(ii) ಎರಡು ಪ್ರತ್ಯೇಕವಾದ ಮತ್ತು ಛೇದಿಸುವ ರೇಖೆಗಳು ಒಂದೇ ರೇಖೆಗೆ ಸಮಾಂತರವಾಗಲು ಸಾಧ್ಯವಿಲ್ಲ.
2.ಯೂಕ್ಲಿಡನ 5ನೇ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯು ಸಮಾಂತರ ರೇಖೆಗಳಿರುವುದನ್ನು ಪ್ರತಿಪಾದಿಸುತ್ತದೆಯೆ? ವಿವರಿಸಿ.
ಪರಿಹಾರ:-
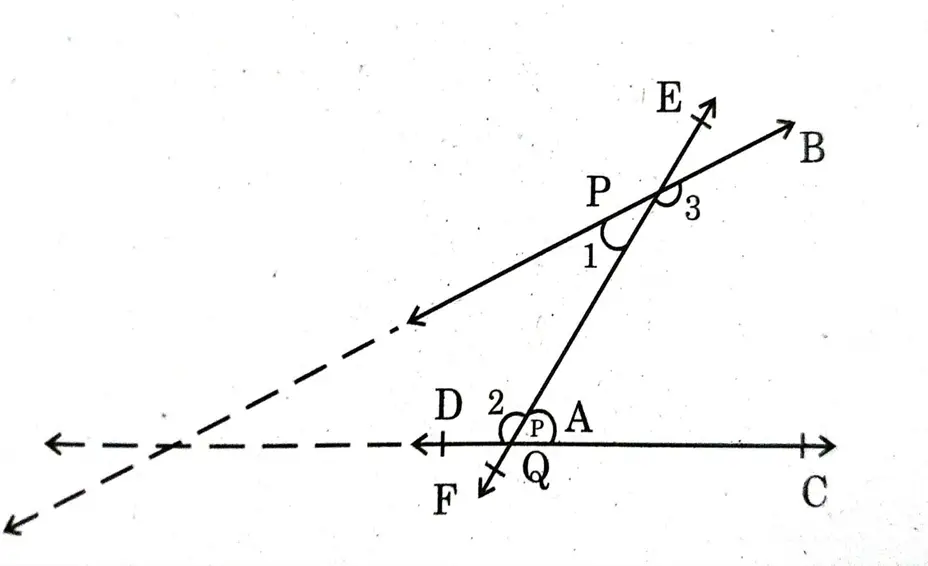
ಯೂಕ್ಲಿಡನ 5ನೇ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯಂತೆ EF ರೇಖಾಖಂಡವು AB ಮತ್ತು CD ಗಳನ್ನು P ಮತ್ತು Q ಗಳಲ್ಲಿ ಛೇದಿಸಿದಾಗ
<1 + <2 <180°.
⇒ < 3+ <4 > 180°.
<1 ಮತ್ತು <2 ರ ಕಡೆಗೆ AB ಮತ್ತು CD ಗಳನ್ನು ವೃದ್ಧಿಸಿದಾಗ ಅವು ಒಂದನ್ನೊಂದು ಸಂಧಿಸುತ್ತವೆ. ಆದ್ದರಿಂದ AB ಯು CD ಗೆ ಸಮಾನಾಂತರವಲ್ಲ.
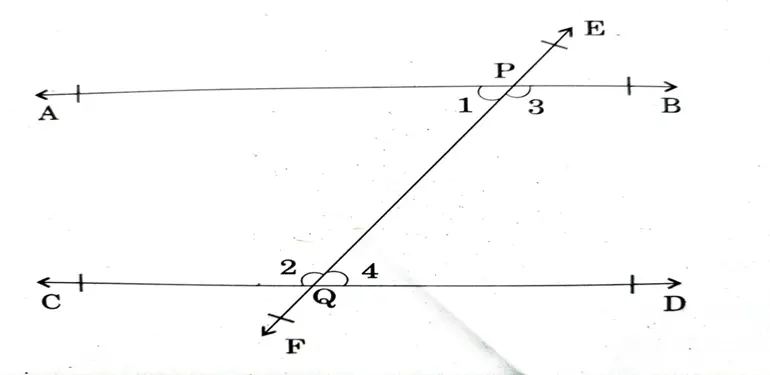
∠1 + <2 = 180° ಆದಾಗ
⇒<3+ <4 = 180°
ಇದರಿಂದ AB ಮತ್ತು CD ಗಳನ್ನು ಎರಡು ಕಡೆಯು ಅನಂತವಾಗಿ ವೃದ್ಧಿಸಿದಾಗ ಅವು ಒಂದನ್ನೊಂದು ಸಂಧಿಸುವುದಿಲ್ಲ.
ಆದ್ದರಿಂದ AB || CD. ಇದರಿಂದ ಯುಕ್ಲಿಡನ 5ನೇ ಆಧಾರ ಪ್ರತಿಜ್ಞೆಯು ಸಮಾಂತರ ರೇಖೆಗಳಿರುವುದನ್ನು ಪ್ರತಿಪಾದಿಸುತ್ತದೆ.