ಪೂರ್ಣಾಂಕಗಳು
ಅಭ್ಯಾಸ 1.1
1. (a) ಮೊತ್ತ -7
(b) ವ್ಯತ್ಯಾಸ -10
(c) ವ್ಯತ್ಯಾಸ 0, ಆಗಿರುವಂತೆ ಒಂದು ಜೊತೆ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಬರೆಯಿರಿ.
(a) − 8 + (+1) = −7
(b) − 12 − (−2) = −10
(c) 5 + (−5) = 0
2. (a) ವ್ಯತ್ಯಾಸ 8 ಆಗುವಂತೆ ಒಂದು ಜೊತೆ ಋಣ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಬರೆಯಿರಿ.
(b) ಮೊತ್ತ -5 ಆಗುವಂತೆ ಒಂದು ಋಣ ಪೂರ್ಣಾಂಕ ಮತ್ತು ಒಂದು ಧನ ಪೂರ್ಣಾಂಕವನ್ನು ಬರೆಯಿರಿ.
(c) ವ್ಯತ್ಯಾಸ -3 ಆಗುವಂತೆ ಒಂದು ಋಣ ಪೂರ್ಣಾಂಕ ಮತ್ತು ಒಂದು ಧನ ಪೂರ್ಣಾಂಕವನ್ನು ಬರೆಯಿರಿ.
(a) −2 − (−10) = 8
(b) −8 + 3 = −5
(c) −2 − (+1) = −3
3. ಒಂದು ರಸಪ್ರಶ್ನೆ ಕಾರ್ಯಕ್ರಮದಲ್ಲಿ ಅನುಕ್ರಮವಾಗಿ ಮೂರು ಸುತ್ತುಗಳಲ್ಲಿ A ತಂಡವು -40, 10, 0 ಅಂಕಗಳನ್ನು ಮತ್ತು B ತಂಡವು 10, 0, -40 ಅಂಕಗಳನ್ನು ಗಳಿಸಿದವು. ಯಾವ ತಂಡವು ಹೆಚ್ಚು ಅಂಕವನ್ನು ಗಳಿಸಿತು? ಯಾವುದೇ ಕ್ರಮದಲ್ಲಿ ನಾವು ಪೂರ್ಣಾಂಕಗಳ ಸಂಕಲನ ಮಾಡಬಹುದೇ?
ಉತ್ತರ:-
ತಂಡ A ನ ಅಂಕ -40, 10, 0.
ಒಟ್ಟು ಅಂಕಗಳು = – 40 + 10 + 0= −30
ತಂಡ B ನ ಅಂಕ 10, 0, −40
ಒಟ್ಟು ಅಂಕಗಳು = 10 + 0 + (-40) = -30
∴ ಎರಡೂ ತಂಡಗಳ ಅಂಕಗಳು ಸಮಾನವಾಗಿವೆ.
ಹೌದು, ನಾವು ಯಾವುದೇ ಕ್ರಮದಲ್ಲಿ ಪೂರ್ಣಾಂಕಗಳ ಸಂಕಲನ ಮಾಡಬಹುದು.
4. ಮುಂದಿನ ಹೇಳಿಕೆಗಳು ಸರಿಹೊಂದುವಂತೆ ಖಾಲಿ ಸ್ಥಳಗಳನ್ನು ಭರ್ತಿಮಾಡಿ:
(i) (− 5) + (− 8) = (− 8) + (…)
(ii) − 53 + … = − 53
(iii) 17 + … = 0
(iv) [13 + (− 12)] + (…) = 13 + [(− 12) + (− 7)]
(v) (− 4) + [15 + (− 3)] = [(− 4) + 15] + —————
ಪರಿಹಾರ:-
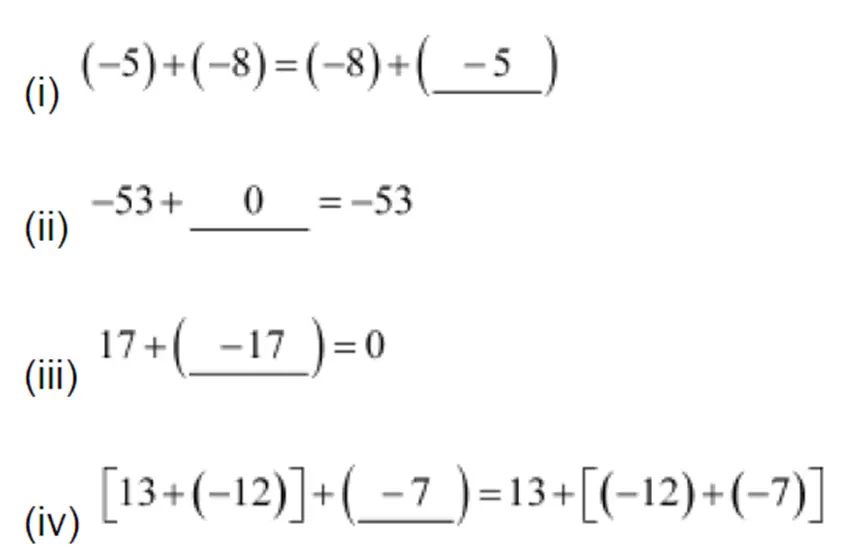
ಅಭ್ಯಾಸ 1.2
- ಪ್ರತಿಯೊಂದರ ಗುಣಲಬ್ಧವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ:
(a) 3 × (–1) (b) (–1) × 225
(c) (–21) × (–30) (d) (–316) × (–1)
(e) (–15) × 0 × (–18) (f) (–12) × (–11) × (10)
(g) 9 × (–3) × (–6) (h) (–18) × (–5) × (–4)
(i) (-1) × (-2) × (-3) × 4 (j) (-3) × (-6) × (-2) × (-1)
ಪರಿಹಾರ:-
(a) 3 × (−1) = −3
(b) (−1) × 225 = −225
(c) (−21) × (−30) = 630
(d) (−316) × (−1) = 316
(e) (−15) × 0 × (−18) = 0
(f) (−12) × (−11) × 10 = 1320
(g) 9 × (−3) × (−6) = 162
(h) (−18) × (−5) × (−4) = −360
(i) (−1) × (−2) × (−3) × 4 = −24
(j) (−3) × (−6) × (−2) × (−1) = 36
2. ಮುಂದಿನವುಗಳನ್ನು ಪರೀಕ್ಷಿಸಿ:
(a) 18 × [7 + (–3)] = [ 18 × 7 ] + [18 × (–3)]
(b) (-21) × [(-4) + (-6)] = [(-21) × (-4)] + [(-21) × (-6)]
ಪರಿಹಾರ:-
(a) L.H.S(ಎಡಬದಿ) = 18 × [7 + (− 3)] = 18 × [7 − 3] = 18 × 4 = 72
R.H.S(ಬಲಬದಿ)= [18 × 7] + [18 × (− 3)] = 126 + (− 54) = 72
∴ 18 × [7 + (–3)] = [ 18 × 7 ] + [18 × (–3)]
(b) L.H.S. (ಎಡಬದಿ) = (−21) × [(−4) + (−6)] = (−21) × [− 4 − 6] = (−21) × [−10] = 210
R.H.S(ಬಲಬದಿ)=. = [(−21) × (−4)] + [(−21) × (−6)] = 84 + 126 = 210
∴ (–21) × [(–4) + (–6)] = [(–21) × (–4)] + [(–21) × (–6)]
3. (i) ಯಾವುದೇ ಪೂರ್ಣಾಂಕ a ಗೆ, (–1) × a ಯಾವುದಕ್ಕೆ ಸಮ?
(ii) (-1) ರೊಂದಿಗೆ ಮುಂದಿನ ಗುಣಲಬ್ಧಗಳನ್ನು ನೀಡುವ ಪೂರ್ಣಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಿ.
(a) -22 (b) 37 (c) 0
(i) ಪ್ರಶ್ನೆಯ ಪ್ರಕಾರ, ಮೂರು ಪ್ರಕರಣಗಳು ಸಾಧ್ಯ ಏಕೆಂದರೆ ನಾವು ಸಂಖ್ಯಾರೇಖೆಯನ್ನು ಋಣಾತ್ಮಕ ಪೂರ್ಣಾಂಕಗಳು ,0 ಮತ್ತು ಧನಾತ್ಮಕ ಪೂರ್ಣಾಂಕಗಳು ಎಂದು ವಿಭಜಿಸಬಹುದು
ಪ್ರಕರಣ 1: a ಯಾವುದೇ ಋಣಾತ್ಮಕ ಪೂರ್ಣಾಂಕ ಆಗಿದ್ದರೆ, ಅಂದರೆ – a,
ಆದಾಗ (−1) × (- a ) = a
ಪ್ರಕರಣ 2: a =0 ಆದಾಗ
(-1) × 0 = 0
ಪ್ರಕರಣ 3: a ಯಾವುದೇ ಧನಾತ್ಮಕ ಪೂರ್ಣಾಂಕವಾಗಿದ್ದಾಗ, ಅಂದರೆ, a,
(-1) × a = -a
ಹೀಗಾಗಿ, ಸಂಭವನೀಯ ಉತ್ತರಗಳು a , 0 ಮತ್ತು -a .
(ii) (a) –22 (b) 37 (c) 0
(a) 22×-1=-22
(b) -37×-1=37
(c) 0×-1=0
4. (–1) × 5 ರಿಂದ ಆರಂಭಿಸಿ, (-1) × (-1) = 1 ವಿನ್ಯಾಸವನ್ನು ಸೂಚಿಸುವ ವಿವಿಧ ಗುಣಲಬ್ಧಗಳನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:- −1 × 5 = −5
−1 × 4 = −4 = − 5 + 1
−1 × 3 = −3 = − 4 + 1
−1 × 2 = −2 = − 3 + 1
−1 × 1 = −1 = − 2 + 1
−1 × 0 = 0 = − 1 + 1
ಆದ್ದರಿಂದ −1 × (−1) = 0 + 1 = 1
ಅಭ್ಯಾಸ 1.3
1. ಮುಂದಿನವುಗಳ ಮೌಲ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(a) (-30) ÷ 10 (b) 50 ÷ (-5)
(c) (-36) ÷ (-9) (d) (-49) ÷ 49
(e) 13 ÷ [(-2) + 1] (f) 0 ÷ (-12)
(g) (-31) ÷ [(-30) + (-1)] (h) [(-36) ÷ 12] ÷ 3
(i) [(-6) + 5] ÷ [(-2) + 1]
ಉತ್ತರ:-
(a) (−30) ÷ 10 = −3
(b) 50 ÷ (−5) = −10
(c) (−36) ÷ (−9) = 4
(d) (−49) ÷ 49 = −1
(e) 13 ÷ [−2 + 1] = 13 ÷ [−1] = −13
(f) 0 ÷ (−12) = 0
(g) (−31) ÷ [(−30) + (−1)] = (−31) ÷ (−31) = 1
(h) [(−36) ÷ 12] ÷ 3 = [−3] ÷ 3 = −1
(i) [− 6 + 5] ÷ [− 2 + 1] = (−1) ÷ (−1) = 1
2. ಮುಂದೆ ನೀಡಿರುವ ಪ್ರತಿ a, b,ಮತ್ತು c ಬೆಲೆಗೆ
a ÷ ( b + c ) ≠ ( a ÷ b ) + ( a ÷ c ) ಎಂಬುದನ್ನು ಪರಿಶೀಲಿಸಿ.
(a) a = 12, b = −4, c = 2
(b) a = (− 10), b = 1, c = 1
ಉತ್ತರ:-
(a) a = 12, b = −4, c = 2
a ÷ ( b + c ) = 12 ÷ (− 4 + 2) = 12 ÷ (−2) = −6
( a ÷ b ) + ( a ÷ c ) = [12 ÷ (−4)] + [12 ÷ 2] = −3 + 6 = 3
ಆದ್ದರಿಂದ, a ÷ ( b + c ) ≠ ( a ÷ b ) + ( a ÷ c )
(b) a = −10, b = 1, c = 1
a ÷ ( b + c ) = (−10) ÷ (1 + 1) = (−10) ÷ 2 = −5
( a ÷ b ) + ( a ÷ c ) = [(−10) ÷ 1] + [(−10) ÷ 1] = − 10 − 10 = −20
ಆದ್ದರಿಂದ, a ÷ ( b + c ) ≠ ( a ÷ b ) + ( a ÷ c )
3. ಖಾಲಿ ಸ್ಥಳ ತುಂಬಿರಿ:
(a) 369 ÷ ___ = 369 (b) (-75) ÷ ___ = -1
(c) (-206) ÷ ___ = 1 (d) -87 ÷ ___ = 87.
(e) ___ ÷ 1 = -87 (f) ___ ÷ 48 = -1.
(g) 20 ÷ ___ = -2 (h) ___ ÷ 4 = 3.
ಉತ್ತರ:-
(a) 369 ÷ 1 = 369 (b) (-75) ÷ 75 = -1
(c) (-206) ÷ 206 = 1 (d) -87 ÷ -1= 87.
(e) -87÷ 1 = -87 (f) -48÷ 48 = -1.
(g) 20 ÷ -10= -2 (h) 12 ÷ 4 = 3.
4. a ÷ b = -3 ಆಗುವಂತೆ ಐದು ಜೊತೆ ಪೂರ್ಣಾಂಕ (a, b) ಗಳನ್ನು ಬರೆಯಿರಿ. ಅಂತಹ ಒಂದು ಜೊತೆ (6, -2) ಏಕೆಂದರೆ, 6 ÷ (-2) =(-3).
ಉತ್ತರ:-
(i) (3, −1)
ಏಕೆಂದರೆ 3 ÷ (−1) = −3
(ii) (−3, 1)
ಏಕೆಂದರೆ (−3) ÷ 1 = −3
(iii) (9, −3)
ಏಕೆಂದರೆ 9 ÷ (−3) = −3
(iv) (−9, 3)
ಏಕೆಂದರೆ (−9) ÷ 3 = −3
(v) (12, −4)
ಏಕೆಂದರೆ 12 ÷ (−4) = −3
5. ಮಧ್ಯಾಹ್ನ 12 ಗಂಟೆಗೆ ಉಷ್ಣತೆಯು ಸೊನ್ನೆಯಿಂದ ಮೇಲೆ 10 °C ಇತ್ತು. ಮಧ್ಯರಾತ್ರಿವರೆಗೆ ಪ್ರತಿ ಗಂಟೆಗೆ 2°C ಯಂತೆ ಇಳಿಕೆಯಾದರೆ, ಯಾವ ಸಮಯದಲ್ಲಿ ಉಷ್ಣತೆಯು ಸೊನ್ನೆಗಿಂತ ಕೆಳಗೆ 8°C ಆಗಬಹುದು? ಮಧ್ಯರಾತ್ರಿಯಲ್ಲಿ ಉಷ್ಣತೆ ಎಷ್ಟಿರುತ್ತದೆ?
ಉತ್ತರ:-
ಆರಂಭಿಕ ಉಷ್ಣತೆ ಅಂದರೆ, ಮಧ್ಯಾಹ್ನ12 ಕ್ಕೆ = 10 ° C
ಪ್ರತಿ ಗಂಟೆಗೆ ಉಷ್ಣತೆಯಲ್ಲಿನ ಬದಲಾವಣೆ = -2 ° C
ಮಧ್ಯಾಹ್ನ 1:00 ಗಂಟೆಗೆ ಉಷ್ಣತೆ = 10ºC + (−2ºC) = 8ºC
ಮಧ್ಯಾಹ್ನ 2:00 ಗಂಟೆಗೆ ಉಷ್ಣತೆ = 8ºC + (−2ºC) = 6ºC
ಮಧ್ಯಾಹ್ನ 3:00 ಗಂಟೆಗೆ ಉಷ್ಣತೆ = 6ºC + (−2ºC) = 4ºC
4:00 PM ನಲ್ಲಿ ಉಷ್ಣತೆ= 4ºC + (−2ºC) = 2ºC
5:00 PM ನಲ್ಲಿ ಉಷ್ಣತೆ = 2ºC + (−2ºC) = 0ºC
6:00 PM ನಲ್ಲಿ ಉಷ್ಣತೆ =0 ºC + (−2 ºC) = −2 ºC
7:00 PM ನಲ್ಲಿ ಉಷ್ಣತೆ = −2 ºC + (−2 ºC) = −4 ºC
8:00 PM ನಲ್ಲಿ ಉಷ್ಣತೆ=−4 ºC + (−2 ºC) = −6 ºC
9:00 PM ನಲ್ಲಿ ಉಷ್ಣತೆ= −6ºC + (−2ºC) = −8ºC
9:00 PM ನಲ್ಲಿ ತಾಪಮಾನ = -6 ºC + (-2 ºC) = -8 ºC
ಆದ್ದರಿಂದ, 9:00 PM ಕ್ಕೆ ಉಷ್ಣತೆಯು ಶೂನ್ಯಕ್ಕಿಂತ 8 ° C ಆಗಿರುತ್ತದೆ.
12:00 ನಂತರ ಮಧ್ಯರಾತ್ರಿ (ಅಂದರೆ, 12:00 AM) ಆಗಲು 12 ಗಂಟೆಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.
12 ಗಂಟೆಗಳಲ್ಲಿ ಉಷ್ಣತೆಯಲ್ಲಿ ಬದಲಾವಣೆ = -2 °C × 12 = -24 ºC
ಮಧ್ಯರಾತ್ರಿಯಲ್ಲಿ, ಉಷ್ಣತೆಯು = 10 + (-24)
= -14°C
ಆದ್ದರಿಂದ, ಮಧ್ಯರಾತ್ರಿಯ ಉಷ್ಣತೆಯು 0 ಕ್ಕಿಂತ ಕಡಿಮೆ 14 ºC ಇರುತ್ತದೆ.
6. ಒಂದು ತರಗತಿ ಪರೀಕ್ಷೆಯಲ್ಲಿ ಪ್ರತಿ ಸರಿ ಉತ್ತರಕ್ಕೆ (+3) ಅಂಕ ಮತ್ತು ಪ್ರತಿ ತಪ್ಪು ಉತ್ತರಕ್ಕೆ (-2) ಅಂಕ ಮತ್ತು ಪ್ರಯತ್ನಿಸದ ಪ್ರಶ್ನೆಗಳಿಗೆ ಯಾವುದೇ ಅಂಕವನ್ನು ನೀಡಿರುವುದಿಲ್ಲ.
(i) ರಾಧಿಕಾ 20 ಅಂಕ ಗಳಿಸಿದಳು. ಅವಳು 12 ಸರಿ ಉತ್ತರ ನೀಡಿದರೆ ಎಷ್ಟು ಪ್ರಶ್ನೆಗಳನ್ನು ತಪ್ಪಾಗಿ ಉತ್ತರಿಸಿದ್ದಳು?
(ii) ಮೋಹಿನಿ ಈ ಪರೀಕ್ಷೆಯಲ್ಲಿ -5 ಅಂಕ ಗಳಿಸುತ್ತಾಳೆ. ಆದಾಗ್ಯೂ ಅವಳು 7 ಸರಿ ಉತ್ತರ ನೀಡಿರುತ್ತಾಳೆ. ಎಷ್ಟು ಪ್ರಶ್ನೆಗಳನ್ನು ಅವಳು ತಪ್ಪಾಗಿ ಉತ್ತರಿಸಿದ್ದಳು?
ಉತ್ತರ:-
ಪ್ರತಿ ಸರಿ ಉತ್ತರಕ್ಕೆ ಪಡೆವ ಅಂಕಗಳು = +3
ಪ್ರತಿ ತಪ್ಪು ಉತ್ತರಕ್ಕೆ ಪಡೆವ ಅಂಕಗಳು = -2
(i) ರಾಧಿಕಾ ಗಳಿಸಿದ ಅಂಕಗಳು = 20
12 ಸರಿಯಾದ ಉತ್ತರಗಳಿಗೆ ಪಡೆದ ಅಂಕಗಳು = 12 × 3 = 36
ತಪ್ಪಾದ ಉತ್ತರಗಳಿಗೆ ಪಡೆದ ಅಂಕಗಳು = ಒಟ್ಟು ಅಂಕಗಳು – 12 ಸರಿ ಉತ್ತರಕ್ಕೆ ಪಡೆದ ಅಂಕಗಳು
= 20 – 36 = -16
ಪ್ರತಿ ತಪ್ಪು ಉತ್ತರಕ್ಕೆ ಪಡೆದ ಅಂಕಗಳು = -2
ಹೀಗಾಗಿ, ತಪ್ಪಾದ ಉತ್ತರಗಳ ಸಂಖ್ಯೆ = (-16) ÷(-2) = 8
ಆದ್ದರಿಂದ, ಅವಳು 8 ಪ್ರಶ್ನೆಗಳನ್ನು ತಪ್ಪಾಗಿ ಉತ್ತರಿಸಿದ್ದಳು.
(ii) ಮೋಹಿನಿ ಗಳಿಸಿದ ಅಂಕಗಳು = −5
7 ಸರಿಯಾದ ಉತ್ತರಗಳಿಗೆ ಪಡೆದ ಅಂಕಗಳು = 7 × 3 = 21
ತಪ್ಪಾದ ಉತ್ತರಗಳಿಗೆ ಪಡೆದ ಅಂಕಗಳು = ಒಟ್ಟು ಅಂಕಗಳು – 7 ಸರಿ ಉತ್ತರಕ್ಕೆ ಪಡೆದ ಅಂಕಗಳು
= – 5 – 21 = -26
ಪ್ರತಿ ತಪ್ಪು ಉತ್ತರಕ್ಕೆ ಪಡೆದ ಅಂಕಗಳು = -2
ಹೀಗಾಗಿ, ತಪ್ಪಾದ ಉತ್ತರಗಳ ಸಂಖ್ಯೆ = (-26) ÷(-2) = 13
ಆದ್ದರಿಂದ, ಅವಳು 13 ಪ್ರಶ್ನೆಗಳನ್ನು ತಪ್ಪಾಗಿ ಉತ್ತರಿಸಿದ್ದಳು.
7. ಒಂದು ಎಲಿವೇಟರ್ ಪ್ರತಿ ನಿಮಿಷಕ್ಕೆ 6m ವೇಗದಲ್ಲಿ ಗಣಿಯೊಳಗೆ ಇಳಿಯುತ್ತದೆ. ಅದು ನೆಲ ಮಟ್ಟದ ಮೇಲೆ 10m ನಿಂದ ಇಳಿಯಲು ಪ್ರಾರಂಭಿಸಿದರೆ -350m ತಲುಪಲು ಎಷ್ಟು ಸಮಯ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ?
ಉತ್ತರ:-
ಆರಂಭಿಕ ಎತ್ತರ = +10 ಮೀ
ಅಂತಿಮ ಆಳ = -350 ಮೀ
ಎಲಿವೇಟರ್ನಿಂದ ಇಳಿಯಬೇಕಾದ ಒಟ್ಟು ದೂರ = (-350) – (+10) = -360 ಮೀ
ಎಲಿವೇಟರ್ ಪ್ರತಿ ನಿಮಿಷಕ್ಕೆ 6m ವೇಗದಲ್ಲಿ ಗಣಿಯೊಳಗೆ ಇಳಿಯುತ್ತದೆ.
ಹೀಗಾಗಿ, ಎಲಿವೇಟರ್ -360 ಮೀ ಇಳಿಯಲು ತೆಗೆದುಕೊಂಡ ಸಮಯ = (-360) ÷ (-6)
= 60 ನಿಮಿಷಗಳು = 1 ಗಂಟೆ